n×n 矩阵计算的 javascript 实现。

# n×n 矩阵计算

# n×n 矩阵

若A = (a[i][j])和B = (b[i][j])为 n × n 的方阵，则对i, j = 1, 2, ..., n，定义乘积C = A · B中的元素c[i][j]为：

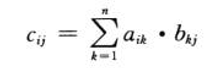
# 基本 js 实现

function squareMatrixMultiply(A, B) {
  var n = A.length;
  var C = [];
  for (var i = 0; i < n; i++) {
    C[i] = [];
    for (var j = 0; j < n; j++) {
      C[i][j] = 0;
      for (var k = 0; k < n; k++) {
        C[i][j] += A[i][k] * B[k][j];
      }
    }
  }
  return C;
}

# 验证

var AMatrix = [[1, 3], [7, 5]];
var BMatrix = [[6, 8], [4, 2]];
squareMatrixMultiply(AMatrix, BMatrix);
// 输出[[18, 14], [62, 66]]

var AMatrix = [[1, 3, 2, 1], [7, 5, 1, 7], [1, 2, 3, 9], [2, 3, 1, 2]];
var BMatrix = [[6, 8, 2, 2], [4, 2, 2, 8], [2, 3, 1, 2], [7, 5, 1, 7]];
squareMatrixMultiply(AMatrix, BMatrix);
// 输出[[29, 25, 11, 37], [113, 104, 32, 105], [83, 66, 18, 87], [40, 35, 13, 44]]

# 分治策略的矩阵算法

# 直接的递归分治算法

思路

js 实现

function squareMatrixMultiplyRecursive(A, B) {
  // 传入原矩阵、复制起点(x, y)、复制长度n
  function getMatrix(M, x, y, n) {
    // console.log(M, x, y, n)
    var N = [];
    for (var i = 0; i < n; i++) {
      N[i] = [];
      for (var j = 0; j < n; j++) {
        // 复制值
        N[i][j] = M[i + y][j + x];
      }
    }
    return N;
  }

  // 方阵的相加, 若传入type为'minus'，则进行减运算
  function addMatrix(A, B, type) {
    var n = A.length;
    var N = [];
    for (var i = 0; i < n; i++) {
      N[i] = [];
      for (var j = 0; j < n; j++) {
        // 复制值
        N[i][j] = type === "minus" ? A[i][j] - B[i][j] : A[i][j] + B[i][j];
      }
    }
    return N;
  }

  // 整理矩阵，将多维数组整理成二维数组
  function convertMatrix(M) {
    // 取出所有值
    var arr = M.toString().split(",");
    var array = [];
    // 选出有效值
    for (var k = 0; k < arr.length; k++) {
      if (arr[k]) {
        array.push(Number(arr[k]));
      }
    }
    // 计算数组长度以及平方根
    var n = array.length;
    var m = Math.sqrt(n);
    // console.log('M', M, n, m)

    // 重新整理为二维数组
    var N = [],
      L = [];
    N[0] = array.slice(0, n / 4);
    N[1] = array.slice(n / 4, n / 2);
    N[2] = array.slice(n / 2, (n * 3) / 4);
    N[3] = array.slice((n * 3) / 4, n);
    for (var i = 0; i < m; i++) {
      L[i] = [];
    }
    for (var l = 0; l < 4; l++) {
      for (var i = 0; i < m / 2; i++) {
        for (var j = 0; j < m / 2; j++) {
          L[i + (Math.floor(l / 2) * m) / 2].push(N[l][j + (i * m) / 2]);
        }
      }
    }
    return L;
  }

  var n = A.length; // 获取长度
  // 创建n×n矩阵C
  var C = [];
  for (var i = 0; i < n; i++) {
    C[i] = [];
  }
  if (n === 1) {
    // 若只有一个数，则返回乘积
    C[0][0] = A[0][0] * B[0][0];
  } else {
    var m = parseInt(n / 2);
    // 分割A为n/2矩阵[[A11, A12], [A21, A22]]
    var A11 = getMatrix(A, 0, 0, m);
    var A12 = getMatrix(A, m, 0, n - m);
    var A21 = getMatrix(A, 0, m, n - m);
    var A22 = getMatrix(A, m, m, m);
    // 分割B为n/2矩阵[[B11, B12], [B21, B22]]
    var B11 = getMatrix(B, 0, 0, m);
    var B12 = getMatrix(B, m, 0, n - m);
    var B21 = getMatrix(B, 0, m, n - m);
    var B22 = getMatrix(B, m, m, m);

    // 递归求出A11, A12, A21, A22以及B11, B12, B21, B22的值
    // 求出矩阵C，并返回
    C[0][0] = addMatrix(
      squareMatrixMultiplyRecursive(A11, B11),
      squareMatrixMultiplyRecursive(A12, B21)
    );
    C[0][1] = addMatrix(
      squareMatrixMultiplyRecursive(A11, B12),
      squareMatrixMultiplyRecursive(A12, B22)
    );
    C[1][0] = addMatrix(
      squareMatrixMultiplyRecursive(A21, B11),
      squareMatrixMultiplyRecursive(A22, B21)
    );
    C[1][1] = addMatrix(
      squareMatrixMultiplyRecursive(A21, B12),
      squareMatrixMultiplyRecursive(A22, B22)
    );
    C = convertMatrix(C);
  }
  return C;
}

验证

var AMatrix = [[1, 3], [7, 5]];
var BMatrix = [[6, 8], [4, 2]];
squareMatrixMultiplyRecursive(AMatrix, BMatrix);
// 输出[[18, 14], [62, 66]]

var AMatrix = [[1, 3, 2, 1], [7, 5, 1, 7], [1, 2, 3, 9], [2, 3, 1, 2]];
var BMatrix = [[6, 8, 2, 2], [4, 2, 2, 8], [2, 3, 1, 2], [7, 5, 1, 7]];
squareMatrixMultiplyRecursive(AMatrix, BMatrix);
// 输出[[29, 25, 11, 37], [113, 104, 32, 105], [83, 66, 18, 87], [40, 35, 13, 44]]

# 矩阵乘法的 Strassen 算法

该算法比较长，大家可参考《算法导论》一书或者Strassen 演算法 ── 分治矩陣乘法 (opens new window)。

思路

2×2 矩阵计算：

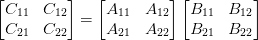
传统的矩阵乘法运算方式，C[i][j] = A[i][1]·B[1][j] + A[i][2]·B[2][j]，总共使用 8 个分块乘法和 4 个分块加法。 Strassen 演算使用 7 个分块乘法和 18 个分块加法：

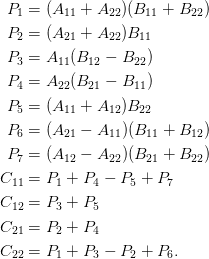
js 实现

function squareMatrixMultiplyStrassen(A, B) {
  // 传入原矩阵、复制起点(x, y)、复制长度n
  function getMatrix(M, x, y, n) {
    var N = [];
    for (var i = 0; i < n; i++) {
      N[i] = [];
      for (var j = 0; j < n; j++) {
        // 复制值
        N[i][j] = M[i + y][j + x];
      }
    }
    // console.log(M,x,y,n,N)
    return N;
  }

  // 方阵的相加, 若传入type为'minus'，则进行减运算
  function addMatrix(A, B, type) {
    var n = A.length;
    var N = [];
    for (var i = 0; i < n; i++) {
      N[i] = [];
      for (var j = 0; j < n; j++) {
        // 复制值
        N[i][j] = type === "minus" ? A[i][j] - B[i][j] : A[i][j] + B[i][j];
      }
    }
    return N;
  }

  // 整理矩阵，将多维数组整理成二维数组
  function convertMatrix(M) {
    // 取出所有值
    var arr = M.toString().split(",");
    var array = [];
    // 选出有效值
    for (var k = 0; k < arr.length; k++) {
      if (arr[k]) {
        array.push(Number(arr[k]));
      }
    }
    // 计算数组长度以及平方根
    var n = array.length;
    var m = Math.sqrt(n);
    // console.log('M', M, n, m)

    // 重新整理为二维数组
    var N = [],
      L = [];
    N[0] = array.slice(0, n / 4);
    N[1] = array.slice(n / 4, n / 2);
    N[2] = array.slice(n / 2, (n * 3) / 4);
    N[3] = array.slice((n * 3) / 4, n);
    for (var i = 0; i < m; i++) {
      L[i] = [];
    }
    for (var l = 0; l < 4; l++) {
      for (var i = 0; i < m / 2; i++) {
        for (var j = 0; j < m / 2; j++) {
          L[i + (Math.floor(l / 2) * m) / 2].push(N[l][j + (i * m) / 2]);
        }
      }
    }
    return L;
  }

  var n = A.length; // 获取长度
  // 创建n×n矩阵C
  var C = [];
  for (var i = 0; i < n; i++) {
    C[i] = [];
  }
  if (n === 1) {
    // 若只有一个数，则返回乘积
    C[0][0] = A[0][0] * B[0][0];
  } else {
    var m = parseInt(n / 2);
    // 分割A为n/2矩阵[[A11, A12], [A21, A22]]
    var A11 = getMatrix(A, 0, 0, m);
    var A12 = getMatrix(A, m, 0, n - m);
    var A21 = getMatrix(A, 0, m, n - m);
    var A22 = getMatrix(A, m, m, m);
    // 分割B为n/2矩阵[[B11, B12], [B21, B22]]
    var B11 = getMatrix(B, 0, 0, m);
    var B12 = getMatrix(B, m, 0, n - m);
    var B21 = getMatrix(B, 0, m, n - m);
    var B22 = getMatrix(B, m, m, m);

    // 计算7个P矩阵
    var P1 = squareMatrixMultiplyStrassen(
      addMatrix(A11, A22),
      addMatrix(B11, B22)
    );
    var P2 = squareMatrixMultiplyStrassen(addMatrix(A21, A22), B11);
    var P3 = squareMatrixMultiplyStrassen(A11, addMatrix(B12, B22, "minus"));
    var P4 = squareMatrixMultiplyStrassen(A22, addMatrix(B21, B11, "minus"));
    var P5 = squareMatrixMultiplyStrassen(addMatrix(A11, A12), B22);
    var P6 = squareMatrixMultiplyStrassen(
      addMatrix(A21, A11, "minus"),
      addMatrix(B11, B12)
    );
    var P7 = squareMatrixMultiplyStrassen(
      addMatrix(A12, A22, "minus"),
      addMatrix(B21, B22)
    );

    // 求出矩阵C，并返回
    C[0][0] = convertMatrix(
      addMatrix(addMatrix(P1, P4), addMatrix(P5, P7, "minus"), "minus")
    );
    C[0][1] = convertMatrix(addMatrix(P3, P5));
    C[1][0] = convertMatrix(addMatrix(P2, P4));
    C[1][1] = convertMatrix(
      addMatrix(addMatrix(P1, P3), addMatrix(P2, P6, "minus"), "minus")
    );
    C = convertMatrix(C);
  }
  return C;
}

验证

var AMatrix = [[1, 3], [7, 5]];
var BMatrix = [[6, 8], [4, 2]];
squareMatrixMultiplyStrassen(AMatrix, BMatrix);
// 输出[[18, 14], [62, 66]]

var AMatrix = [[1, 3, 2, 1], [7, 5, 1, 7], [1, 2, 3, 9], [2, 3, 1, 2]];
var BMatrix = [[6, 8, 2, 2], [4, 2, 2, 8], [2, 3, 1, 2], [7, 5, 1, 7]];
squareMatrixMultiplyStrassen(AMatrix, BMatrix);
// 输出[[29, 25, 11, 37], [113, 104, 32, 105], [83, 66, 18, 87], [40, 35, 13, 44]]

写着玩的，认真你就输了哈哈。

← 8. 分治法求最大子数组 1. 认识数据库 →